Archive for November, 2008
Now that December has arrived you may well be thinking of sending your loved ones a Christmas card so why not send them one based on some sort of Mathematics? Even better – why not design it yourself? Software packages such as Mathematica, SAGE and MATLAB are absolutely perfect for this sort of thing since they combine a large amount of mathematical functionality with top quality plotting routines. To see what I mean – let’s take a look at a Christmas greeting designed by the developers of the open source mathematical system, SAGE.

I have to confess that I do not have a clue about the mathematics behind the above greeting (something to do with a p-adic plot function apparently) but maybe by the time Christmas comes around I will understand how it was created. The SAGE source code you need to generate it is
sage: P1 = Zp(3).plot(rgbcolor=(0,1,0))
sage: P2 = Zp(7).plot(rgbcolor=(1,0,0))
sage: P3 = text("$Seasons$ $Greetings$ ",(0.0,1.8))
sage: P4 = text("$from$ $everyone$ $at$ sagemath.org!",(0.1,-1.6))
sage: (P1+P2+P3+P4).show(axes=False)
I thought I would have at doing one and came up with the design below by re-using some Mathematica code from a Wolfram Demonstration. The design is based on a fractal called the Koch Snowflake.
Koch[0] = {{0, 0}, {1, 0}, {1/2, -(Sqrt[3]/2)}, {0, 0}} // N;
Koch[n_] := Koch[n] =
Module[{s},
Partition[Koch[n - Sign[n]], 2, 1] /. {a_, b_} :> (s = b - a;
{a, a + s/3, a + s/3 + RotationTransform[Sign[n] 60 °][s/3],a + 2 s/3})] //
Append[Flatten[#, 1], Last[Koch[n - Sign[n]]]] &;
Graphics[Line@Koch[5],
Epilog -> Inset[Style["Merry Christmas", 20], {Center, Center}, {Center,Center}]]

OK, so it’s clear that I am no designer but how often do you get a Christmas card that comes complete with Source code? This got me thinking, there must be people out there with better design skills than me – a great many of them in fact and so onto the challenge.
Your task is to design a Christmas message with a mathematical theme using any mathematical system or programming language of your choice. Your design must be generated algorithmically (so you can’t design it in Photoshop and import it into Mathematica for example) and it must include source code. Ideally, you should include a quick explanation of the mathematics you featured in your design.
There will be no prizes I’m afraid other than kudos and praise from me but hopefully you’ll have fun doing it just the same. You can get your designs to me in a number of ways: email me, post source code in the comments section or post your design on your own website and send me the link – whatever you feel is best.
If you do not have access to a commercial maths package such as Mathematica, MAPLE or MATLAB then I suggest that you take a look at SAGE which is completely free (in fact you should take a look at SAGE even if you DO have one of the commercial systems).
Assuming some people actually respond to this post, I will post some of my favourites over the run up to Christmas.
Have fun!
I have just installed SAGE 3.2 on my Ubuntu 8.10 machine and received the following error message.
It looks like jsMath failed to set up properly (error code -7). I will try to keep going, but it could get ugly.
I discovered a forum thread that suggested that installing jsmath-fonts would fix the problem
apt-get install jsmath-fonts
but, unfortunately, it didn’t. I found that I also had to install ttf-jsmath
apt-get install ttf-jsmath
A quick restart of firefox later and SAGE looked very pretty indeed!
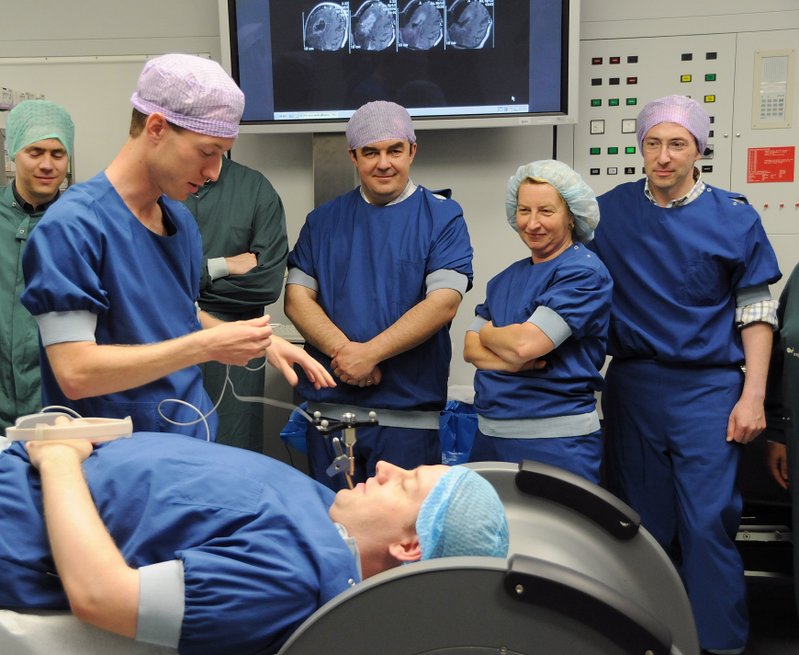
Many people have referred to me as brainless over the years so when offered the opportunity to prove otherwise at the International Mathematica Symposium earlier this year I jumped at the chance.
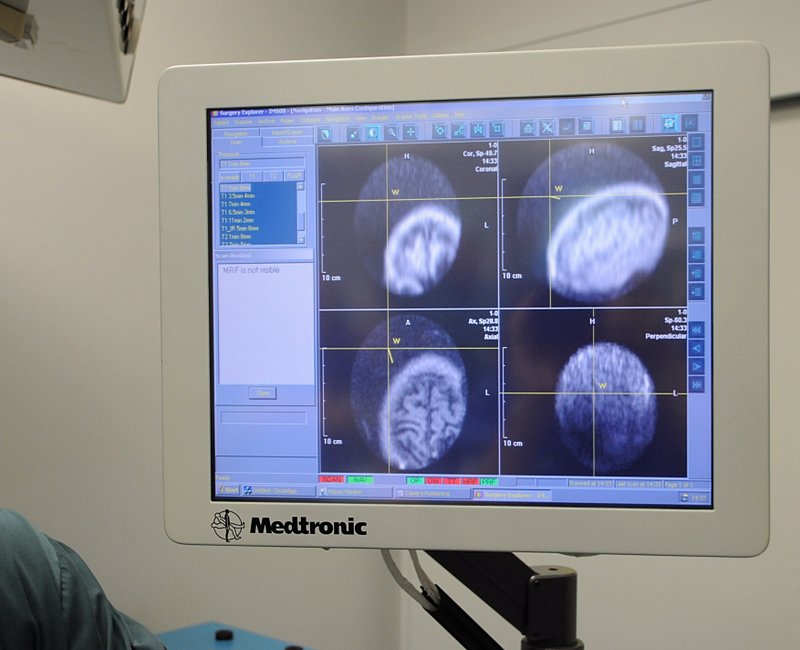
Apparently the reason for the fuzziness in the image was because I moved around too much during the scan. This could have been fixed but it would have involved bolting my skull into position and, although the crowd were interested in a demonstration, I was not really that up for it.
If I remember the details correctly, this is a low resolution scanner that can be used by surgeons while brain surgery is actually taking place. Although a surgeon would have access to very high resolution scans, taken before surgery begins, these would steadily become inaccurate due to changes made to the brain during surgery.
Thanks to Barrie Stokes for the pictures.
A friend of mine pointed out that I haven’t yet made any nominations for this year’s Edublog awards so here they are.
My nomination for the Best Resource Sharing Blog 2008 is The Teaching College Math Technology Blog which is written by Maria Andersen. The amount of technology that can be applied to teaching in mathematics is truly staggering from Mathematica through to technologies such as GraphPad, Windows 7, Interactive Tables and Jing. Maria not only informs us of these technologies but she actually uses them in her teaching and reports on the results – what works, what doesn’t, what is useful and what could be made better. With so much cool stuff to play with, it almost makes me wish I was a Maths teacher.
My other nomination is for the Best Group Blog 2008 and the nominee is 360. 360 is an unofficial Blog of the Nazareth College Math Department in Rochester, New York and it offers a wide range of interesting mathematical tidbits. I find myself returning to 360 again and again since they manage to simulatenously entertain and inform on the subject of mathematics. For example – in the last month alone they have written articles on (among other things) Copernicus, geometry puzzles, kenKen, Pythagorean Triples and how fourier transforms were used to answer questions about a song by the Beatles. Quite simply – one of my favourite maths blogs.
It’s that time of year again – a time when your thoughts naturally turn to what Christmas presents you might buy for the geek in your life. If you are a geek yourself then this is an easy exercise – just think what you might want yourself and buy that. Geeks know what other geeks like you see!
What if you are not a geek though? How do you work out what your nerdy friend would like most for Christmas? What you need, dear reader, is a geek guide – someone of the nerdy persuasion who can help you separate the geek wheat from the nerd chaff.
Now if you have read much of my blog you will have probably come to the conclusion that I am a geek (or possibly a nerd – the difference is subtle) and so maybe you are thinking that I can help you. Well, maybe I can – but only for a certain type of geek.
You see, there are many varieties of geek and each one has different needs and wants, thus making it impossible to write a post entitled “Christmas gifts for geeks” which will please everyone. So, I am going to concentrate on gifts for the mathematically inclined which includes (but is not limited to) mathematicians, scientists, engineers and, most importantly…..me! Many of my friends read this blog and so this post is mainly a shameless hint dropping exercise but it is possible that it will be of use to other people as well.
In addition, if you actually buy any of these books using the links in this post then I will earn some commission from Amazon without it costing you a penny extra. Doing this helps support Walking Randomly and is greatly appreciated but I really won’t mind if you choose not to.
Books
For the mathematician in your life you almost certainly cannot go wrong by buying them a book – just make sure that they haven’t already got it! Another tip is ‘don’t try to be too specialised’ – advanced textbooks may well be useful but they are not (often) much fun and Christmas presents are supposed to be fun!
With these thoughts in mind I will separate this section into two parts – books I own and books I wish I owned. In addition, I will only consider the lighter side of the mathematical spectrum (for a given value of ‘lighter’) so these books should be of interest to mathematicians of any level – from high school students to research scientists. The large number of equations that some of them contain may make them look like text books in some cases, but let me assure you that they are (mostly) easy reading.
Books I own – and highly recommend
- “e”, The Story of a Number
by Eli Maor. Some numbers are so important that they get whole books written about them and e (sometimes known as Euler’s number) is one of them. It’s a constant that certainly gets around as it appears in all manner of places from compound interest to calculus with detours through subjects such as complex analysis and trigonometry. This book is easy to read and contains a mixture of mathematics, history and biography.
- An Imaginary Tale: The Story of “i”
by Paul Nahin. I’ll never forget the look on my dad’s face when he asked what I was learning at University and I told him ‘they are teaching us about imaginary numbers.’ It didn’t exactly strengthen his faith in further education I can tell you! It turns out that the term ‘imaginary’ is an unfortunate byproduct of history and if you delve into the mathematics then you’ll soon learn that not only do imaginary numbers exist but that they form the basis of one of the most beautiful and powerful areas of mathematics there is.
- Gamma: Exploring Euler’s Constant
by Julian Havil. Everyone has heard of Pi, quite a few people know about e but you’ll be hard pressed to find a non-mathematician who knows about Gamma. Impress the mathmo in your life by giving them a book about a mathematical constant that has been seriously undersold by its PR team. It contains some heavier mathematics than the books mentioned above but it is still accessible to good high school students and undergraduates. I’m still working my way through it to be honest and loving every minute.
- Flatland: A Romance of Many Dimensions
by Edwin Abbott. We live in a three dimensional world world (some say 4, some say 11 but for the sake of this note I am saying 3) but what would it be like if we inhabited a world of only 2 dimensions. Imagine how life would be in such a world and how we would react to a mysterious visitor from the 3rd dimension. Edwin Abbott did exactly this and in the process wrote a satire on Victorian England (the book was written in 1884, making this a very early example of science fiction). This is a very charming (and very cheap) book that was first recommended to me by a fellow physicist.
- The Music of the Primes
by Marcus du Sautoy. Prime numbers fascinate us, there can be no denying that, and in this book Marcus takes us to meet some of the people and mathematics behind them. Some reviewers complain about the fact that the mathematics isn’t detailed enough but then others may well say that it is too mathematical – writing popular maths books is a difficult game. Personally I think he had it just right and told a great story with just enough maths to keep it from being a book on history rather than a book on maths . Whenever I wanted more detail I looked to other sources and this got me reading more books on number theory. This is precisely what popular maths books should do in my opinion – invite the reader in….show them enough to whet their appetite but not so much that it scares them off, point them in the direction of further study and leave them wanting more….
- The Man Who Loved Only Numbers
by Paul Hoffman. This is a book about the life of an extremely eccentric mathematician called Paul Erdős – one of the most prolific writers in mathematics apparently. Erdős was a strange character but an extremely well respected mathematician. This book is serious easy reading and contains a lot less actual math than most of the other books I mention here. I have a copy in my office and many people have borrowed and enjoyed it – only one of them was a mathematician by training. This is a great book. In fact I am going to read it again on the train home this evening.
- Inside Your Calculator: From Simple Programs to Significant Insights
by Gerald Rising. “Sir, how does the calculator know the sine of a number?” I innocently asked my teacher at the end of a maths lesson back when I was far too young to have a scientific calculator. He blustered for a bit before answering ‘It stores them in memory – it’s just a big look up table’. I was deeply suspicious. That would take a lot of memory I thought! A lot more than my cheapo calculator had that’s for sure. So how do calculators do this stuff? This book makes a good job of explaining the detail (hint…CORDIC).
- Surely You’re Joking, Mr.Feynman!
by Leighton, Feynman and Hutchings. Richard Feynman is an all time hero of mine and this book is a collection of anecdotes about his life. If memory serves me there is not a single equation in this book but I would be surprised to meet a mathememtican who doesn’t enjoy it. Wanna see the human side of a genius? Buy this book then.
Books I wish I owned (feel free to buy one for me if your mood takes you that way.)
- The Princeton Companion to Mathematics
Edited by Timothy Gowers (click here for his blog) – This beautiful looking book is for the more serious mathematician but it is the sort of thing that will remain on their bookshelf for years to come. Essentially it is a guide to as much pure mathematics as you can fit into a single volume and would be a perfect addition to any mathematicians library. It’s a bit expensive but looks like it’s worth every penny.
- Hexaflexagons, Probability Paradoxes, and the Tower of Hanoi
by Martin Gardner. Martin is something of a legend among recreational mathematicians and has many books and articles to his name. He wrote the ‘mathematical games’ column for Scientific American for many years where he picked up a large following among mathematicians at all levels. This book is a collection of some of the best of his Scientific American articles that have been expanded with updates and new material. Even if you only have a passing interest in mathematics – this looks like a good book to get.
- Bad Science
I feel like I know Ben Goldacre well and yet I have never met him but his blog and column in the Guardian have kept me entertained and informed for years. An expert in refuting dodgy statistics and sham science, Ben takes no prisoners. I find his writing extremely entertaining as well as providing much food for thought so naturally I would like his book. Where is the maths connection? Well, maths is often abused by the media and it’s often statistics that gets abused. Ben tends to have a lot to say about that.
- An Adventurer’s Guide to Number Theory
by Richard Friedberg. I have no idea what this book might be like but I enjoy number theory, I like the title, it gets good reviews and it’s reasonably priced. Sounds good to me.
- Digital Dice Computational Solutions to Practical Probability Problems
by Paul Nahin. I have a couple of Nahin’s books and they are both great so I am guessing this one will be just as good. From what I have seen, he includes lots of simulations in MATLAB. Randomness? MATLAB? Nahin? Of course I want this book.
- Nonplussed: Mathematical Proof of Implausible Ideas
by Julian Havil. There are a lot of true facts in Mathematics that make you say ‘no way – that can’t be true’ when you first hear them. I have said this to myself several times over the years and it usually takes a good, solid proof (along with several concrete examples) before I concede the point. By the sound of it this book is choc full of this sort of thing.
- Euler’s Gem: The Polyhedron Formula and the Birth of Topology
by David Richeson. Euler’s name seems to be everywhere in mathematics – you only need to look at this list from Wikipedia to get an idea of just how pervasive his ideas have become. I have never seen this book and I don’t know much about his polyhedron formula but I do intend to find out.
- The Drunkard’s Walk: How Randomness Rules Our Lives
by Leonard Mlodinow. When you write a blog called ‘Walking Randomly’ you really should have some books about randomness on your shelf. That’s partly why this one is here. The good reviews don’t do any harm either.
Version 7 of Wolfram Research’s flagship product, Mathematica, has been released today – just 18 months after version 6. I have been fiddling with beta versions of it for a while now and have been desperate to start talking about it but the NDA I signed prevented me from doing so until today.
A full review will have to wait because, paradoxically, I don’t have access to the full version of Mathematica 7 right now but here are a few highlights that got my attention during beta testing.
Built in Parallel Computing
The computer I am typing this blog post on is nothing special by today’s standards and yet it is a quad-core machine which effectively means that it contains not 1 but 4 CPUs. Most pieces of software tend to only use one of these cores which means that the other 3 are sitting about doing nothing most of the time. It’s a bit like being assigned a team of helpers to help you work on a project and then saying to 3 of them – “You guys can just sit around doing nothing because I don’t know how to use you.” Pretty shoddy management huh? Ideally, what you need to do is to parallelize your algorithm so those other 3 cores can get off their backsides and do something useful.
Previous versions of Mathematica had limited support for making use of multi-core machines like mine. As far as I know they were limited to relatively low level matrix and vector operations that made use of underlying BLAS and LAPACK libraries. I had a brief forum discussion with some people on this topic a while back but never got around to following it up.
If you wanted to write fully parallel code with previous versions of Mathematica then you needed to buy a separate product called the Parallel Computing Toolkit. Most people who expressed an interest in parallel Mathematica at my university soon lost interest when they realised that they would have to spend more money to make it work.
In Version 7, Wolram have done the right thing and have built in a whole suite of commands and frameworks to allow you to fully parallelize your Mathematica code. Now, finally, you can make use of the spare cores in your computer. There will be follow up blog posts on this topic I can assure you (just as soon as I figure out how to do it all!)
Image Processing
While at the International Mathematica Symposium in Maastricht I saw my first demonstration of version 7 and one of the things that caught my attention was the range of image processing features that Wolfram were building into the product. In the demonstration, the speaker was manipulating photographs in Mathematica exactly as you might manipulate any other mathematical expression. In other words you could give the photograph itself as the argument to a function! There was no messing around with file handles or input streams or whatever – you just wrapped the picture in a function and pressed enter. For example (images used with permission from Wolfram Research) – The following input

Gives the following output

Wolfram have also added a whole suite of image manipulation algorithms and so with just a few commands even someone like me (who knows nothing about image processing) could write fully interactive image processing applications. I imagine that this would be extremely useful for the academics I work for as well as being a lot of fun for me (can anyone recommend a good book that teaches about image processing algorithms by the way).
Delay Differential Equations
Mathematica now has built in support for delay differential equations and my boss used to do research into these a few years ago so we’ll have yet another topic to talk about. I note that MATLAB has support for these too and so a future comparison might be interesting.
Improved charting
Mathematica has always been able to do things like Pie charts, bar charts and the like but they have never been as good as other areas of Mathematica’s plotting functionality such as 2 and 3D function plots. In version 7, this area of visualization has been vastly improved.
More, More more
Version 7 is the first major version of Mathematica that I have covered since starting this blog and I have to say I am a little overwhelmed with the quantity of improvements that Wolfram have made. Up until now I have only talked about minor releases such as 6.0.3 and 6.0.2 where I could cover pretty much all of the new functionality in a single blog post – with version 7 I have no chance. There is just too much to include all at once.
Finally, my friend Maria over at TCMTB has discussed a new Mathematica 7 feature that I wasn’t even aware of: The Classroom Assistant. Head over there to see what she has to say about it.
Expect to see a lot more in-depth articles about Mathematica 7 on Walking Randomly in the future. Any requests?
Earlier this year I wrote about a wonderful freeware game called Crayon Physics which was a demo version of an in-development game called Crayon Physics Deluxe. The game’s developer, Petri Purho, wrote the demo in just one week and it caused a small sensation on the internet (and in my office for that matter).
Since then, Petri has been hard at work on the full version of Crayon Physics Deluxe and has been constantly bothered by the game’s fans as to when it will be ready. Petri’s answer is one I approve of – ‘It will be released when it’s done.’ The good news is that Petri feels that it will be done sooner rather than later and has recently set up a site to take pre-orders for the software at the discounted price of $14.95 during Novemer 2008 (the full price will be $20).
Petri – my pre order will be with you at some point over the next few days. Physics has never looked so fun!
Crayon Physics Deluxe from Petri Purho on Vimeo.
If you enjoyed this article, feel free to click here to subscribe to my RSS Feed.
If you double click on a MATLAB .m file on a Windows machine then it will open the file in the MATLAB editor by default. So how do you get similar behaviour in Linux you might ask? This question was recently posed on the MATLAB users group and since no one gave an answer I thought I would have a go and see what I could come up with. After all, how hard could it be?
I’ll cut a long story short and just tell you the solution. To be specific the following tip works on Ubuntu 8.10 running GNOME 2.24.1 but I imagine that a similar procedure would work for some other setups as well.
- Right click on any .m file you like and, in the menu, click on Open With->Open With Other Application
- Click on the arrow to the left of Use a custom command
- In the resulting dialogue box type
matlab -desktop -r "edit %f"
- Click on Open
MATLAB will start up and then the editor will open your file. In future you will not need to type the above command because GNOME will have added an extra item to the Open With menu – namely Open with “matlab”
Hope this helps someone out there and, as always, comments are welcome.
If you enjoyed this article, feel free to click here to subscribe to my RSS Feed.
Walking Randomly was hacked yesterday which caused me (and probably some of my visitors) all manner of problems. Fortunately for me, this site is hosted by an extremely competent team – www.virtualconstruction.co.uk – who moved very quickly to repair the damage caused. I highly recommend them for any web design / hosting work you might need by the way. If they are good enough for clients such as the BBC and The University of Manchester then they are good enough for little old me.
The Wolfam Demonstrations project has just topped 4000 submissions! I make no secret of the fact that I love the Wolfram Demonstrations project and barely a day goes by where I don’t mention it to someone. It’s got so bad that I am sometimes accused of being a secret employee of Wolfram Research (I’m not – just for the record – but they are free to make me an offer.) If you are new around here then here is a quick summary of why I like it so much.
- Over 4000 demonstrations covering a very wide range of disciplines.
- Every demonstration is fully interactive and can be used for free via the Mathematica player.
- Full Mathematica source code for every demonstration is easily available. So, if you have a full copy of Mathematica then you can modify them for your own purposes.
- Everyone who has a fully licensed copy of Mathematica can contribute. This is a true community project.
- The guys and gals at Wolfram vet each and every one of the submissions to ensure that they meet various guidelines. If you are an author of a demonstration then they give advice on how you might improve your submission. Sometimes they even supply code that you might not have been able to come up with yourself.
In my opinion, the project really is all things to all people. For example, if you are a teacher then you might use some of the demonstrations to spice up your courses at no cost. Remember – you can download the free Mathematica Player and use all of the demonstrations fully interactively. There is no need to buy a Mathematica license! I often hear maths educators say “The only way to learn mathematics is to do mathematics.” and they are absolutely right! The Wolfram Demonstrations project gives you and your students another way to ‘do math’. Have you just taught some Fourier analysis? Well then, you might be interested in some examples of Fourier Series or maybe you would like to discuss (and demonstrate) Fourier sound synthesis. You might decide to demonstrate how the Fourier Transform can be used for image compression or maybe show the problems that Fourier series have with discontinuites.
If none of the demonstrations do quite what you want then download the source code and modify them. If you don’t have a full copy of Mathematica or the required programming skills then send a request to Wolfram and they may be able to help. Alternatively ask me – I’ll help whenever I can and have done so in the past both for readers of this blog and for teachers and researchers at my place of work (The University of Manchester).
If you are learning how to use Mathematica and prefer to learn from examples then the project is perfect. 4000+ real-world examples right at your fingertips. For free! I have used Mathematica for over 8 years now and yet I constantly come across new techniques and ideas by reading the source code of other author’s submissions.
Perhaps you are not a programmer or a teacher and you just like fiddling around with Mathematics? Again, the Wolfram Demonstrations project is for you. You might choose to play a relaxing game of Tangrams or challenge your brain with Sudoku. Alternatively you be interested in some of the mathematics behind prime numbers or perhaps you want to play around with polygonal numbers?
So, what would you like to see? Although there are over 4000 different demonstrations so far, there is still a lot of stuff left to cover. What is your personal wish list for the Demonstrations project? If you ask you might get ;)
If you enjoyed this article, feel free to click here to subscribe to my RSS Feed.