Archive for October, 2012
Of Mathematica and memory
A Mathematica user recently contacted me to report a suspected memory leak, wondering if it was a known issue before escalating it any further. At the beginning of his Mathematica notebook he had the following command
Clear[Evaluate[Context[] <> "*"]]
This command clears all the definitions for symbols in the current context and so the user expected it to release all used memory back to the system. However, every time he re-evaluated his notebook, the amount of memory used by Mathematica increased. If he did this enough times, Mathematica used all available memory.
Looks like a memory leak, smells like a memory leak but it isn’t!
What’s happening?
The culprit is the fact that Mathematica stores an evaluation history. This allows you to recall the output of the 10th evaluation (say) with the command
%10
As my colleague ran and re-ran his notebook, over and over again, this history grew without bound eating up all of his memory and causing what looked like a memory leak.
Limiting the size of the history
The way to fix this issue is simply to limit the length of the output history. Personally, I rarely need more than the most recently evaluated output so I suggested that we limit it to one.
$HistoryLength = 1;
This fixed the problem for him. No matter how many times he re-ran his notebook, the memory usage remained roughly constant. However, we observed (in windows at least) that if the Mathematica session was using vast amounts of memory due to history, executing the above command did not release it. So, you can use this trick to prevent the history from eating all of your memory but it doesn’t appear to fix things after the event…to do that requires a little more work. The easiest way, however, is to kill the kernel and start again.
Links
- Memory Management in Mathematica
- Mathematica Session History
- ClearSystemCache[] – The system cache is another area of Mathematica that can use up some memory.
MATLAB Mobile has been around for Apple devices for a while now but Android users have had to make do with third party alternatives such as MATLAB Commander and MLConnect. All that has now changed with the release of MATLAB Mobile for Android.
MATLAB Mobile is NOT MATLAB running on your phone
While MATLAB Mobile is a very nice and interesting product, there is one thing you should get clear in your mind– this is not a full version of MATLAB on your phone or Tablet. MATLAB Mobile is essentially a thin client that connects to an instance of MATLAB running on your desktop or The Mathworks Cloud. In other words, it doesn’t work at all if you don’t have a network connection or a licensed copy of MATLAB.
What if you do want to run MATLAB code directly on your phone?
While it is unlikely that we’ll see a full version of MATLAB compiled for Android devices any time soon, Android toting MATLABers have a couple of other options available to them in addition to MATLAB Mobile.
- Octave for Android Octave is a free, open source alternative to MATLAB that can run many .m file scripts and functions. Corbin Champion has ported it to Android and although it is still a work in progress, it works very well.
- Mathmatiz – Small and light, this free app understands a subset of the MATLAB language and can do basic plotting.
- Addi – Much smaller and less capable than Octave for Android, this is Corbin Champion’s earlier attempt at bringing a free MATLAB clone to Android. It is based on the Java library, JMathLib.
Simulink from The Mathworks is widely used in various disciplines. I was recently asked to come up with a list of alternative products, both free and commercial.
Here are some alternatives that I know of:
- MapleSim – A commercial Simuink replacement from the makers of the computer algebra system, Maple
- OpenModelica -An open-source Modelica-based modeling and simulation environment intended for industrial and academic usage
- Wolfram SystemModeler – Very new commercial product from the makers of Mathematica. Click here for Wolfram’s take on why their product is the best.
- xcos – This free Simulink alternative comes with Scilab.
I plan to keep this list updated and, eventually, include more details. Comments, suggestions and links to comparison articles are very welcome. If you have taught a course using one of these alternatives and have experiences to share, please let me know. Similarly for anyone who was switched (or attempted to switch) their research from Simulink. Either comment to this post or contact me directly.
I’ve nothing against Simulink but would like to get a handle on what else is out there.
There are many ways to benchmark an Android device but the one I have always been most interested in is the Linpack for android benchmark by GreeneComputing. The Linpack benchmarks have been used for many years by supercomputer builders to compare computational muscle and they form the basis of the Top 500 list of supercomputers.
Linpack measures how quickly a machine can solve a dense n by n system of linear equations which is a common task in scientific and engineering applications. The results of the benchmark are measured in flops which stands for floating point operations per second. A typical desktop PC might acheive around 50 gigaflops (50 billion flops) whereas the most powerful PCs on Earth are measured in terms of petaflops (Quadrillions of flops) with the current champion weighing in at 16 petaflops, that’s 16,000,000,000,000,000 floating point operations per second–which is a lot!
Acording to the Android Linpack benchmark, my Samsung Galaxy S2 is capable of 85 megaflops which is pretty powerful compared to supercomputers of bygone eras but rather weedy by today’s standards. It turns out, however, that the Linpack for Android app is under-reporting what your phone is really capable of. As the authors say ‘This test is more a reflection of the state of the Android Dalvik Virtual Machine than of the floating point performance of the underlying processor.’ It’s a nice way of comparing the speed of two phones, or different firmwares on the same phone, but does not measure the true performance potential of your device.Put another way, it’s like measuring how hard you can punch while wearing huge, soft boxing gloves.
Rahul Garg, a PhD. student at McGill University, thought that it was high time to take the gloves off!
rgbench – a true high performance benchmark for android devices
Rahul has written a new benchmark app called RgbenchMM that aims to more accurately reflect the power of modern Android devices. It performs a different calculation to Linpack in that it meaures the speed of matrix-matrix multiplication, another common operation in sicentific computing.
The benchmark was written using the NDK (Native Development Kit) which means that it runs directly on the device rather than on the Java Virtual Machine, thus avoiding Java overheads. Furthermore, Rahul has used HPC tricks such as tiling and loop unrolling to squeeze out the very last drop of performance from your phone’s processor . The code tests about 50 different variations and the performance of the best version found for your device is then displayed.
When I ran the app on my Samsung Galaxy S2 I noted that it takes rather longer than Linpack for Android to execute – several minutes in fact – which is probably due to the large number of variations its trying out to see which is the best. I received the following results
- 1 thread: 389 Mflops
- 2 threads: 960 Mflops
- 4 threads: 867.0 Mflops
Since my phone has a dual core processor, I expected performance to be best for 2 threads and that’s exactly what I got. Almost a Gigaflop on a mobile phone is not bad going at all! For comparison, I get around 85 Mflops on Linpack for Android. Give it a try and see how your device compares.

Links
- RgbenchMM on GooglePlay
- Prelim Analysis of RgbenchMM – Some of the in-depth details of the benchmark, written by the app’s author.
- Supercomputers vs mobile phones
I felt like playing with Julia and MATLAB this Sunday morning. I found some code that prices European Options in MATLAB using Monte Carlo simulations over at computeraidedfinance.com and thought that I’d port this over to Julia. Here’s the original MATLAB code
function V = bench_CPU_European(numPaths) %Simple European steps = 250; r = (0.05); sigma = (0.4); T = (1); dt = T/(steps); K = (100); S = 100 * ones(numPaths,1); for i=1:steps rnd = randn(numPaths,1); S = S .* exp((r-0.5*sigma.^2)*dt + sigma*sqrt(dt)*rnd); end V = mean( exp(-r*T)*max(K-S,0) )
I ran this a couple of times to see what results I should be getting and how long it would take for 1 million paths:
tic;bench_CPU_European(1000000);toc V = 13.1596 Elapsed time is 6.035635 seconds. >> tic;bench_CPU_European(1000000);toc V = 13.1258 Elapsed time is 5.924104 seconds. >> tic;bench_CPU_European(1000000);toc V = 13.1479 Elapsed time is 5.936475 seconds.
The result varies because this is a stochastic process but we can see that it should be around 13.1 or so and takes around 6 seconds on my laptop. Since it’s Sunday morning, I am feeling lazy and have no intention of considering if this code is optimal or not right now. I’m just going to copy and paste it into a julia file and hack at the syntax until it becomes valid Julia code. The following seems to work
function bench_CPU_European(numPaths) steps = 250 r = 0.05 sigma = .4; T = 1; dt = T/(steps) K = 100; S = 100 * ones(numPaths,1); for i=1:steps rnd = randn(numPaths,1) S = S .* exp((r-0.5*sigma.^2)*dt + sigma*sqrt(dt)*rnd) end V = mean( exp(-r*T)*max(K-S,0) ) end
I ran this on Julia and got the following
julia> tic();bench_CPU_European(1000000);toc() elapsed time: 36.259000062942505 seconds 36.259000062942505 julia> bench_CPU_European(1000000) 13.114855104505445
The Julia code appears to be valid, it gives the correct result of 13.1 ish but at 36.25 seconds is around 6 times slower than the MATLAB version. The dog needs walking so I’m going to think about this another time but comments are welcome.
Update (9pm 7th October 2012): I’ve just tried this Julia code on the Linux partition of the same laptop and 1 million paths took 14 seconds or so:
tic();bench_CPU_European(1000000);toc() elapsed time: 14.146281957626343 seconds
I built this version of Julia from source and so it’s at the current bleeding edge (version 0.0.0+98589672.r65a1 Commit 65a1f3dedc (2012-10-07 06:40:18). The code is still slower than the MATLAB version but better than the older Windows build
Update: 13th October 2012
Over on the Julia mailing list, someone posted a faster version of this simulation in Julia
function bench_eu(numPaths)
steps = 250
r = 0.05
sigma = .4;
T = 1;
dt = T/(steps)
K = 100;
S = 100 * ones(numPaths,1);
t1 = (r-0.5*sigma.^2)*dt
t2 = sigma*sqrt(dt)
for i=1:steps
for j=1:numPaths
S[j] .*= exp(t1 + t2*randn())
end
end
V = mean( exp(-r*T)*max(K-S,0) )
end
On the Linux partition of my test machine, this got through 1000000 paths in 8.53 seconds, very close to the MATLAB speed:
julia> tic();bench_eu(1000000);toc() elapsed time: 8.534484148025513 seconds
It seems that, when using Julia, one needs to unlearn everything you’ve ever learned about vectorisation in MATLAB.
Update: 28th October 2012
Members of the Julia team have been improving the performance of the randn() function used in the above code (see here and here for details). Using the de-vectorised code above, execution time for 1 million paths in Julia is now down to 7.2 seconds on my machine on Linux. Still slower than the MATLAB 2012a implementation but it’s getting there. This was using Julia version 0.0.0+100403134.r0999 Commit 099936aec6 (2012-10-28 05:24:40)
tic();bench_eu(1000000);toc() elapsed time: 7.223690032958984 seconds 7.223690032958984
- Laptop model: Dell XPS L702X
- CPU:Intel Core i7-2630QM @2Ghz software overclockable to 2.9Ghz. 4 physical cores but total 8 virtual cores due to Hyperthreading.
- RAM: 8 Gb
- OS: Windows 7 Home Premium 64 bit and Ubuntu 12.04
- MATLAB: 2012a
- Julia: Original windows version was Version 0.0.0+94063912.r17f5, Commit 17f50ea4e0 (2012-08-15 22:30:58). Several versions used on Linux since, see text for details.
Welcome to the latest edition of A Month of Math Software where I take a look at all that is shiny and new in the computational mathematics world. This one’s slightly late and so it not only covers all of September but also the first 3 days in October. If you have any math software news that you’d like to share with the world, drop me a line and tell me all about it. Enjoy!
MATLAB gets a Ribbon (sorry…Toolstrip)
A new version of MATLAB has been released and it has had some major cosmetic surgery. The Mathworks insist on calling the new look in 2012b a Toolstrip but everyone else will call it a Ribbon. Although they’ve been around for many years, ribbon based interfaces hit the big time when Microsoft used them for Office 2007..a decision that many, many, many, many, many, many, many people hated. I hate them too and now I have to contend with one in MATLAB…and so do you because there is no way to switch back to the old interface. The best you can do is minimise the thing and pretend it doesn’t exist. Unhappy users abound (check out the user comments at http://blogs.mathworks.com/loren/2012/09/12/the-matlab-r2012b-desktop-part-1-introduction-to-the-toolstrip/ for example). There have been a lot of other changes too which I’ll discuss in an upcoming review.
Do you use MATLAB? How do you feel about this new look?
Numerical Javascript!
- Numeric, a comprehensive free numerical library for Javascript, has seen a minor update to version 1.2.3. The new release includes a much faster algorithm for linear programming.
Free and open source general purpose mathematics
- Scilab, arguably the best open source MATLAB clone available, has seen a major upgrade to version 5.4. Go to http://www.scilab.org/products/scilab/download/5.4.0/whatsnew for the new goodness.
- On 8th September, Sage version 5.3 was released. Sage is an extremely powerful general purpose mathematics package based on Python and dozens of other open source projects. The Sage development team like to say that instead of re-inventing the wheel they built a car! Mighty fine one too if you ask me. What’s new in Sage 5.3
- René Grothmann has updated his very nice, free Euler Math Toolbox. At the time of writing its at version 18.8 but the updates come thick and fast. The latest changes are always at http://euler.rene-grothmann.de/Programs/XX%20-%20Changes.html
The theory of numbers
- Pari version 2.5.3 has been released. Pari is a free ‘computer algebra system designed for fast computations in number theory’
- Magma version 2.18-10 was released in September. Magma is a commercial system for algebra, number theory, algebraic geometry and algebraic combinatorics.
Numerical Libraries
- The Intel Math Kernel Library (MKL) is now at version 11.0. The MKL is a highly optimised numerical library for Intel platforms that covers subjects such as linear algebra, fast fourier transforms and random numbers. Find out what’s new at http://software.intel.com/en-us/articles/whats-new-in-intel-mkl/
- LAPACK, the standard library for linear algebra on which libraries such as MKL and ACML are based, has been updated to version 3.4.2. There is no new functionality, this is a bug-fix release
- The Numerical Algorithms Group (NAG) have released a major update to their commercial C library. Mark 23 of the library includes lots of new stuff (345 new functions) such as a version of the Mersenne Twister random number generator with skip-ahead, additional functions for multidimensional integrals, a new suite of functions for solving boundary-value problems by an implementation of the Chebyshev pseudospectral method and loads more. The press release is at http://www.nag.co.uk/numeric/CL/newatmark23 and the juicy detail is at http://www.nag.co.uk/numeric/CL/nagdoc_cl23/html/genint/news.html
Python
- After the publication of the last Month of Math Software I learned about the death of John Hunter, author of matplotlib, due to complications arising from cancer treatment. A tribute has been written by Fernando Perez. My heart goes out to his family and friends.
- After 8 months work, version 0.11 of SciPy is now available. Go to http://docs.scipy.org/doc/scipy/reference/release.0.11.0.html for the good stuff which includes improvements to the optimisation routines and new routines for dense and sparse matrices among others.
- A new major release of pandas is available. Pandas provides easy-to-use data structures and data analysis tools for Python. See what’s new in 0.9.0 at http://pandas.pydata.org/pandas-docs/dev/whatsnew.html
Bits of this and that
- IDL version has been bumped to version 8.2.1. http://idldatapoint.com/2012/10/03/idl-8-2-1-released/ has the details.
- Gnumeric version 1.11.6 – A free spreadsheet program
And finally….
I am a big fan of the xkcd webcomic and so a recent question on the Mathematica StackExchange site instantly caught my eye. Xkcd often publishes hand drawn graphs that look like this:
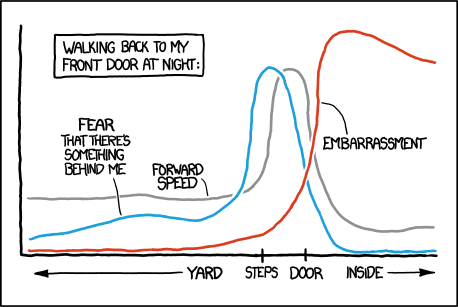
The question asked…How could one produce graphs that look like this using Mathematica? It didn’t take long before the community came up with some code that automatically produces plots like this
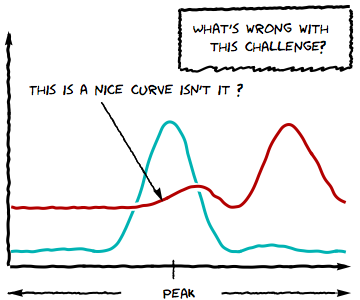
I am definitely going to use style in my next presentation! Not to be out-done, others have since done similar work in R, MATLAB and Latex.