Fun with Graphene from the Wolfram Demonstrations project
I work at The University of Manchester in the UK and, as some of you may have heard, two of our Professors recently won the Nobel Prize in physics for their discovery of graphene. Naturally, I wanted to learn more about graphene and, as a fan of Mathematica, I turned to the Wolfram Demonstrations Project to see what I could see. Click on the images to go to the relevant demonstration.
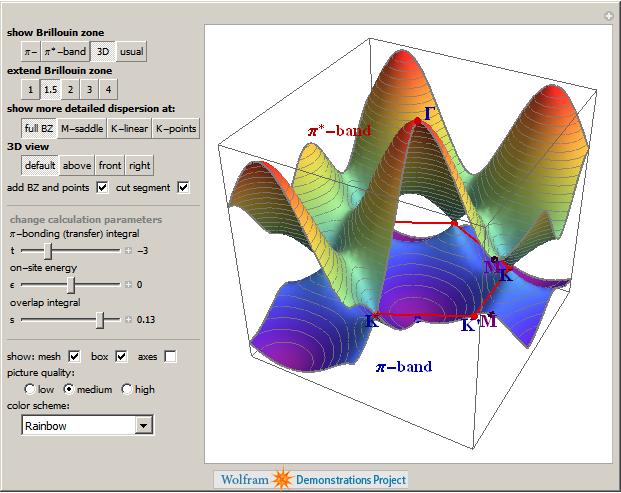
Back when I used to do physics research myself, I was interested in band structure and it turns out that there is a great demonstration from Vladimir Gavryushin that will help you learn all about the band structure of graphene using the tight binding approximation.
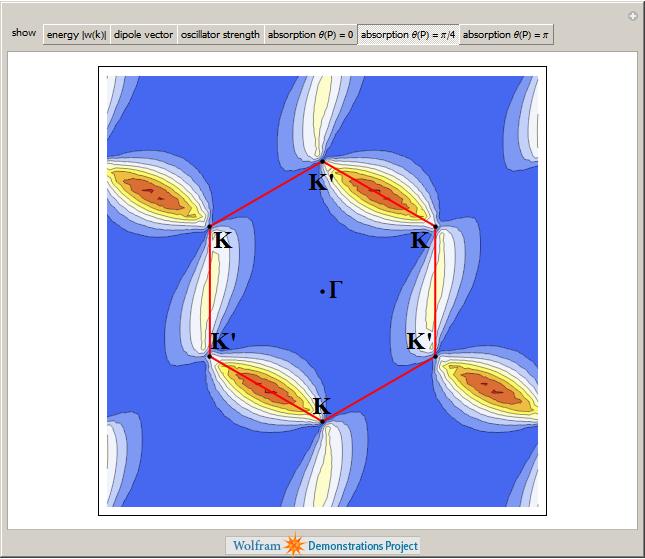
The electronic band structure of a material is important because it helps us to understand (and maybe even engineer) its electronic and optical properties and if you want to know more about its optical properties then the next demonstration from Jessica Alfonsi is for you.
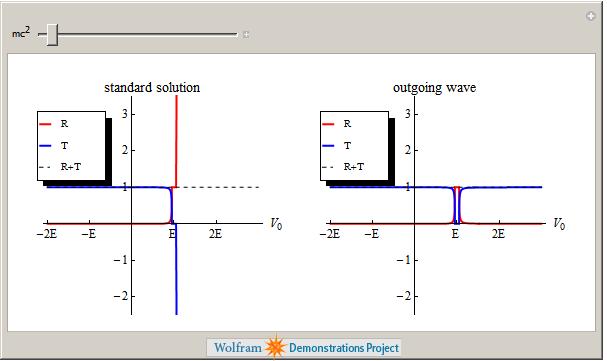
Another professor at Manchester, Niels Walet, produced the next demonstration which asks “Is there a Klein Paradox in Graphene?”
Finally, Graphene can be rolled up to make Carbon Nanotubes as demonstrated by Sándor Kabai.
This is just a taster of the Graphene related demonstrations available at The Wolfram Demonstrations project (There are 11 at the time of writing) and I have no doubt that there will be more in the future. Many of them are exceptionally well written and they include lists of references, full source code and, best of all, they can be run for free using the Mathematica Player.
Don’t just read about cutting-edge research, get in there and interact with it!