Search Results
Back in May 2009, just after Wolfram Alpha was released, I had a look to see which fractals had been implemented. Even at that very early stage there were a lot of very nice fractals that Wolfram Alpha could generate but I managed to come up with a list of fractals that Wolfram Alpha appeared to know about but couldn’t actually render.
On a whim I recently revisited that list and am very pleased to note that every single one of them has now been fully implemented! Very nice.
Can you find any Wolfram Alpha fractals that I missed in the original post?
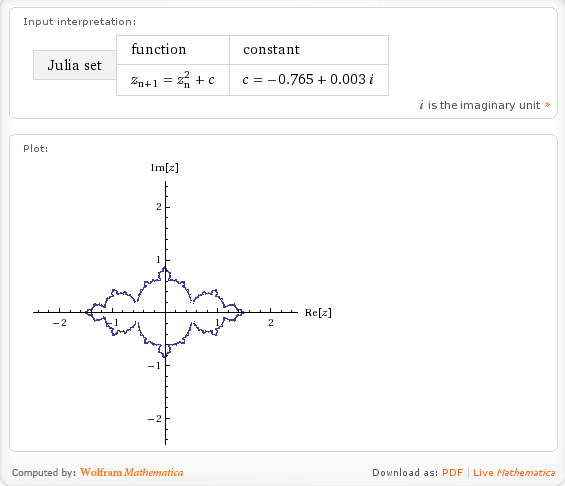
I saw a tweet from someone this morning which mentioned that you could plot the Julia Set using Wolfram Alpha. I had to try this for myself as soon as I could and, sure enough, you can plot the Julia set for any complex number Z: -0.765+0.003 I for example.
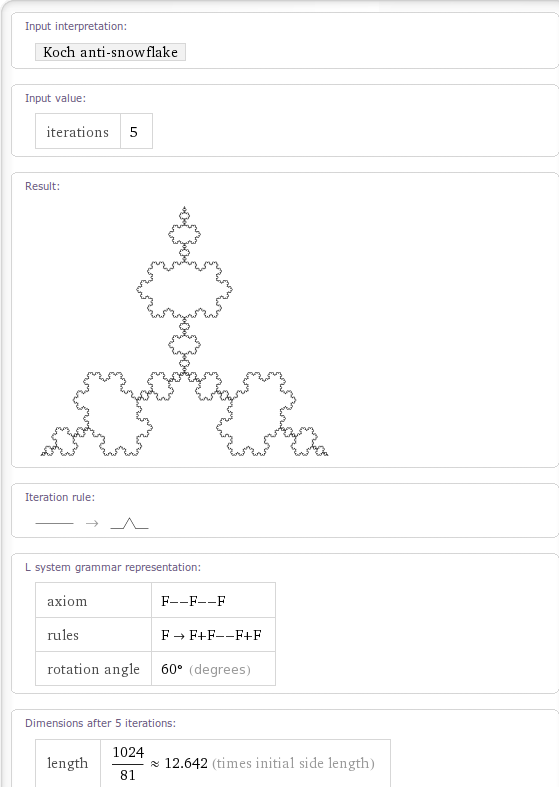
Very nice but what else can it do. If I Walpha fractals then I get the following output so I’d expect Wolfram Alpha to compute at least the Koch snow flake, the Sierpinski gasket, the Haferman carpet and the curlicue fractal and, sure enough, it does (click on the links to see for yourself)
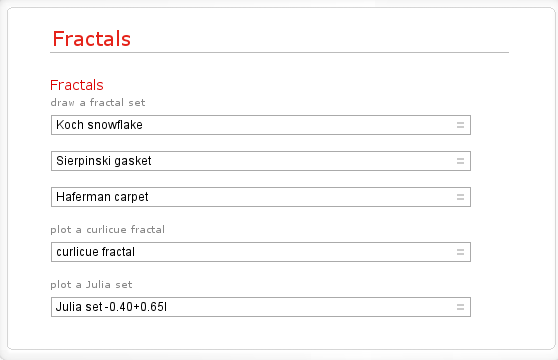
Here is a screenshot for the Koch Fractal.
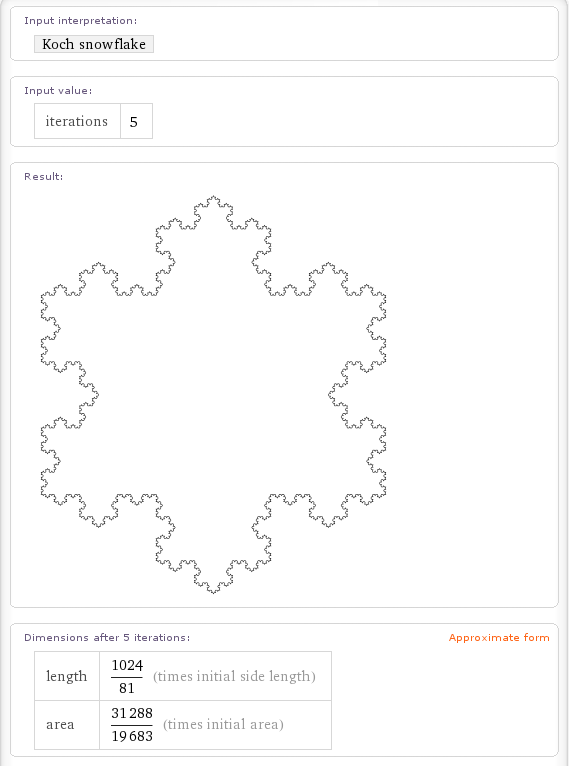
These aren’t the only fractals it knows about though. If you walpha Pentaflake (a fractal close to my heart) then you get the following.
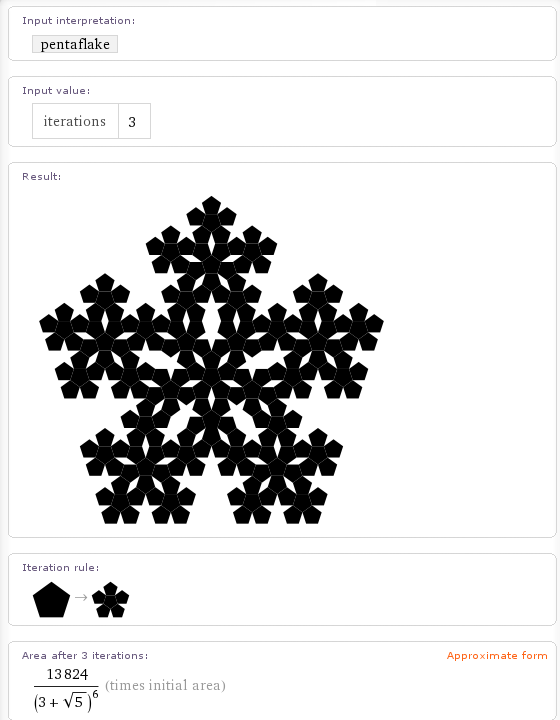
Wolfram Alpha can also calculate the H-Fractal.
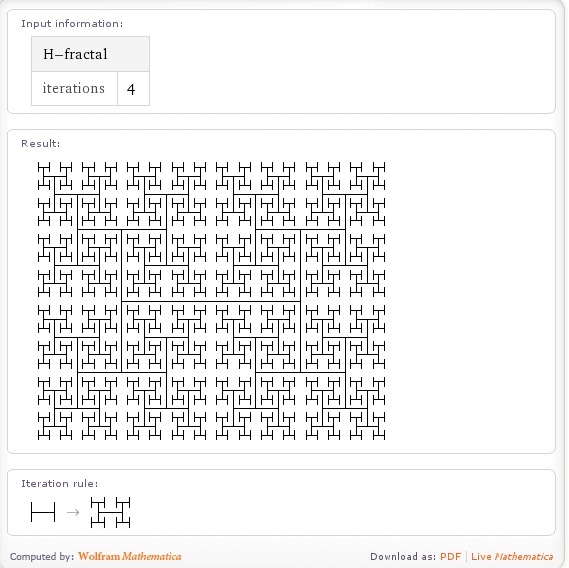
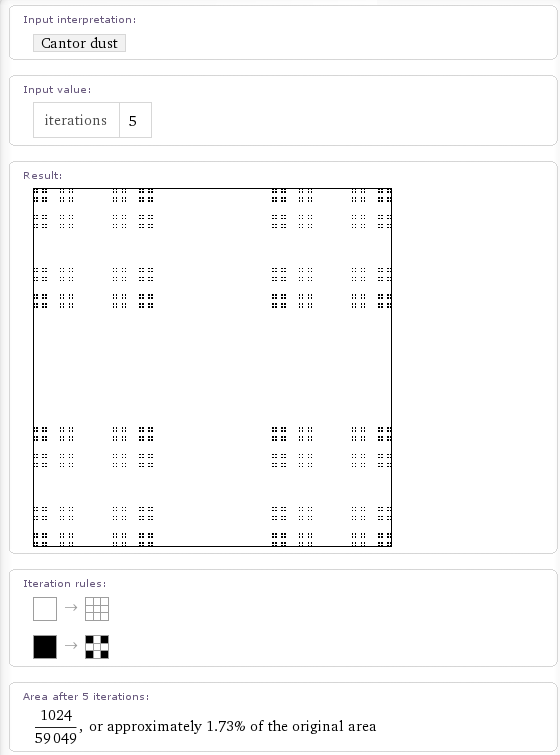
Cantor dust is in there too
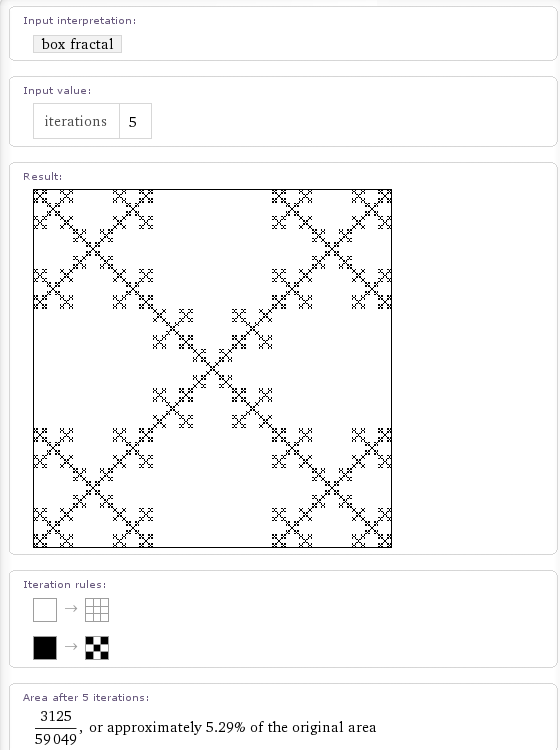
as is the box fractal
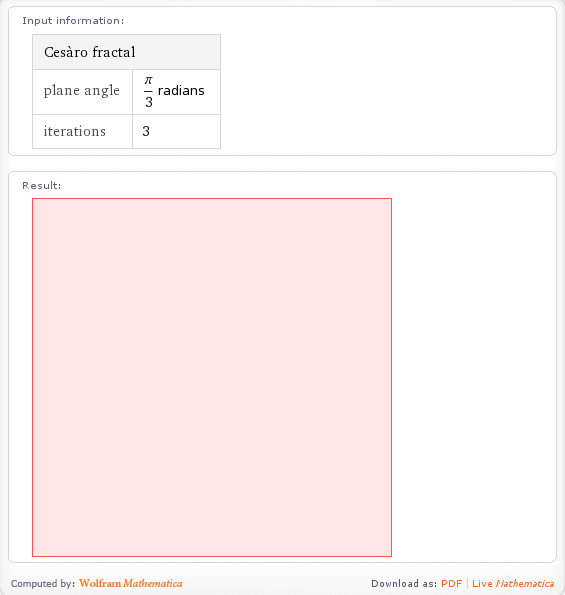
It also looks like they are in the middle of implementing the Cesaro fractal. If you walpha the term then it tries to generate the fractal for a phase angle of pi/3 radians and 5 iterations. A few seconds later and the calculation times out. If you lower the number of iterations it returns a red box such as the one below. If my memory serves, Mathematica returns such a box if there is a problem with the graphics output. I hope to see this fixed soon.
Update:15th July 2009 – The Cesaro Fractal has now been fixed)
It also seems to know about the following fractals but doesn’t seem to calculate anything for them (yet). I say that it seems to know about them because it gives you an input field for ‘Iterations’ which implies that it knows that a number of iterations makes sense in this context. It’ll be cool to see all of these implemented in time.
(Note: None of these are implemented yet and may never be – I’ll update if that changes)
- Menger Sponge Update 21st December 2010 – this has now been implemented
- Gosper Island Update:15th July 2009 – this has now been implemented
- Apollonian Gasket Update 21st December 2010 – this has now been implemented
- Dragon Curve Update 21st December 2010 – this has now been implemented
- Hilbert Curve Update 21st December 2010 – this has now been implemented
- Peano curve Update 21st December 2010 – this has now been implemented
- Cantor Set Update:15th July 2009 – this has now been implemented
Some odd omissions (at the time of writing) are the Mandelbrot set (Update: 15th July 2009 – this has been done now) and the Lorenz attractor.
This is all seriously cool stuff for Fractal fans and shows the power of the Wolfram Alpha idea. Let me know if you discover any more Fractals that it knows about and I’ll add them here.
Update: I’ve found a few more computable fractals in Wolfram Alpha. Please forgive me for the lack of screenshots but this is getting to be a rather graphic-intensive post. The links will take you to a Wolfram Alpha query.
The guys at Blinkdagger put together a great MATLAB Christmas card for you all and sent it in to me as part of the Walking Randomly Christmas challenge. I would have posted it earlier but I have been away from the Internet over Christmas (sorry Rob). Thanks guys!

A brief explanation of the maths involved (from Rob of Blinkdagger)
– the snowdrifts are sine waves of different amplitudes and offsets
– the tree is a 3D spiral of green asterisks
– the ornaments are a random selection of the same points as the tree,
with different colors and marker types
– the presents under the tree are the trademark “membrane” surface that is the MATLAB logo.
– the star atop the tree, as well as the star in the sky are just single points graphed, but using the default marker types creatively
– the text is, well it’s just text
% Xmas card from blinkdagger.com for the challenge
%% setup the fig
h1 = figure(‘Position’,[50 50 800 600],’Color’,’w’);
%% Put background snowdrifts and star
axes(‘Position’,[0 0.5 1 .05]);
ezplot(‘sin(.1*x+1.8)’); axis off; title(”);
axes(‘Position’,[0 0.4 1 .1]);
ezplot(‘sin(.3*x)’); axis off; title(”);
axes(‘Position’,[0 0.25 1 .1]);
ezplot(‘sin(.4*x-1.5)’); axis off; title(”);
axes(‘Position’,[0 0.1 1 .15]);
ezplot(‘cos(.4*x-2)’); axis off; title(”);
axes(‘Position’,[0.75 0.75 0.2 0.2]);
plot(1,1,’x’,’markersize’,48,’markeredgecolor’,[.5 .5 .5]);
axis off; title(”); hold on;
plot(1,1,’h’,’markersize’,36,’markeredgecolor’,[.5 .5 .5]);
plot(1,1,’+’,’markersize’,80,’markeredgecolor’,[.5 .5 .5]);
hold off;
%% Put tree on and decorate it
axes(‘Position’,[0.55 0.2 0.4 0.6]);
z = 0:.05:100;
x = cos(z); x = (101-z).*x;
y = sin(z); y = (101-z).*y;
plot3(x,y,z,’g*’,’markersize’,18); axis off; view(0,10);
hold all;
% star on top
plot3(0,0,107,’p’,’markersize’,24,’markerfacecolor’,[1 .8431 0],…
‘markeredgecolor’,’r’);
% plot ornaments
k = rand(size(x));
k1 = k>.97;
k2 = k>.94 & k<.97;
k3 = k>.91 & k<.94;
k4 = k>.88 & k<.91;
k5 = k>.85 & k<.88;
k6 = k>.82 & k<.85;
plot3(x(k1),y(k1),z(k1),’ro’,’markersize’,8,’linewidth’,2); axis off; view(0,10);
plot3(x(k2),y(k2),z(k2),’ys’,’markersize’,8,’linewidth’,2); axis off; view(0,10);
plot3(x(k3),y(k3),z(k3),’md’,’markersize’,8,’linewidth’,2); axis off; view(0,10);
plot3(x(k4),y(k4),z(k4),’b^’,’markersize’,8,’linewidth’,2); axis off; view(0,10);
plot3(x(k5),y(k5),z(k5),’kh’,’markersize’,8,’linewidth’,2); axis off; view(0,10);
plot3(x(k6),y(k6),z(k6),’c*’,’markersize’,8,’linewidth’,2); axis off; view(0,10);
hold off;
%% Put presents under the tree
axes(‘Position’,[0.5 0.12 0.1 0.15]);
colormap(hot*.7); surf(membrane,membrane); shading flat; axis off; view(300,20);
axes(‘Position’,[0.57 0.1 0.1 0.15]);
surf(membrane); shading flat; axis off; view(300,20);
axes(‘Position’,[0.63 0.08 0.1 0.15]);
surf(membrane); shading flat; axis off; view(300,20);
axes(‘Position’,[0.7 0.08 0.1 0.15]);
surf(membrane); shading flat; axis off; view(300,20);
axes(‘Position’,[0.77 0.1 0.1 0.15]);
surf(membrane); shading flat; axis off; view(300,20);
axes(‘Position’,[0.83 0.13 0.1 0.15]);
surf(membrane); shading flat; axis off; view(300,20);
%% Overlay snowflakes
%% Text greeting
axes(‘Position’,[.05 .6 .5 .5]); axis off;
text(.08,.55,’Seasons Greetings!’,’fontsize’,30,’color’,’r’,…
‘fontname’,’Garamond’,’fontweight’,’bold’);
text(.07,.31,’Best wishes and have a great 2009′,’fontsize’,20,…
‘color’,[0 .4 0],’fontname’,’Garamond’);
text(.07,.18,’solving problems with MATLAB!’,’fontsize’,20,…
‘color’,[0 .4 0],’fontname’,’Garamond’);
text(.07,.05,’From everyone at blinkdagger.com!’,’fontsize’,20,…
‘color’,[0 .4 0],’fontname’,’Garamond’);
Since setting the Walking Randomly Christmas Challenge, I have been looking around the web for Christmasy things that other people have written using mathematical software. If you have been thinking of submitting something to the challenge then maybe these will give you inspiration.
First up, we have several Wolfram Demonstrations based on themes that could be used to design Christmas greeting cards. For example there is a great one by Michael Trott and Jeff Bryant called Decorative Holiday Stars.
If you prefer your greetings less ‘designer’ and more purely Mathematical then how about creating a card from Eisenstein Snowflakes?
Other Wolfram Demonstrations that might give you inspiration for the Christmas challenge include
I next turned my attention to MATLAB and their File Exchange and immediately hit upon a MATLAB file by Marc Lätzel that draws a Christmas tree.

Something a bit more mathematical is the .m file by Per Sundqvist which generates a FEMLAB geometry for the Koch snowflake. This can then be used in FEMLAB to solve eigenvalue problems over the Koch domain. I don’t have a copy of FEMLAB (called COMSOL these days) so I can’t test it but the result looks nice and a quick google search has resulted in some references that might be useful in implementing calculations like this. ‘Computing eigenfunctions on the Koch Snowflake: a new grid and symmetry‘ by John M Neuberger might be a good place to start.
Next up is Maple. A quick search of their Application Centre resulted in the Maple 5 code for a swinging snowman – very nice! This is another one I can’t test because, unfortunately, I don’t have a copy of Maple but if you are one of those who do then the source code is available if you’d like to try it out. Maple is at version 12 these days so it will be interesting to see if this old Maple 5 code still runs (let me know if you are able to test it).

These above examples are just highlights of the sort of thing I discovered while looking around for ‘Christmas maths.’ Why not try your hand at designing something yourself in the Walking Randomly Christmas Challenge? Submissions can be in pretty much any language you care to mention although, of the commercial maths packages, I can only test scripts written in Mathematica, Mupad, MATLAB and MathCAD. Of course any open-source package (such as SAGE or Octave) is fair game.
If you prefer your submission to be anonymous then either don’t let me know who you are (post your code in the comments section for example) or just tell me that you would prefer it if your name were not attached. Of course if you want full recognition for your talents then I can do that too :) My email address is relatively easy to find. Have fun!
Now that December has arrived you may well be thinking of sending your loved ones a Christmas card so why not send them one based on some sort of Mathematics? Even better – why not design it yourself? Software packages such as Mathematica, SAGE and MATLAB are absolutely perfect for this sort of thing since they combine a large amount of mathematical functionality with top quality plotting routines. To see what I mean – let’s take a look at a Christmas greeting designed by the developers of the open source mathematical system, SAGE.

I have to confess that I do not have a clue about the mathematics behind the above greeting (something to do with a p-adic plot function apparently) but maybe by the time Christmas comes around I will understand how it was created. The SAGE source code you need to generate it is
sage: P1 = Zp(3).plot(rgbcolor=(0,1,0))
sage: P2 = Zp(7).plot(rgbcolor=(1,0,0))
sage: P3 = text("$Seasons$ $Greetings$ ",(0.0,1.8))
sage: P4 = text("$from$ $everyone$ $at$ sagemath.org!",(0.1,-1.6))
sage: (P1+P2+P3+P4).show(axes=False)
I thought I would have at doing one and came up with the design below by re-using some Mathematica code from a Wolfram Demonstration. The design is based on a fractal called the Koch Snowflake.
Koch[0] = {{0, 0}, {1, 0}, {1/2, -(Sqrt[3]/2)}, {0, 0}} // N;
Koch[n_] := Koch[n] =
Module[{s},
Partition[Koch[n - Sign[n]], 2, 1] /. {a_, b_} :> (s = b - a;
{a, a + s/3, a + s/3 + RotationTransform[Sign[n] 60 °][s/3],a + 2 s/3})] //
Append[Flatten[#, 1], Last[Koch[n - Sign[n]]]] &;
Graphics[Line@Koch[5],
Epilog -> Inset[Style["Merry Christmas", 20], {Center, Center}, {Center,Center}]]

OK, so it’s clear that I am no designer but how often do you get a Christmas card that comes complete with Source code? This got me thinking, there must be people out there with better design skills than me – a great many of them in fact and so onto the challenge.
Your task is to design a Christmas message with a mathematical theme using any mathematical system or programming language of your choice. Your design must be generated algorithmically (so you can’t design it in Photoshop and import it into Mathematica for example) and it must include source code. Ideally, you should include a quick explanation of the mathematics you featured in your design.
There will be no prizes I’m afraid other than kudos and praise from me but hopefully you’ll have fun doing it just the same. You can get your designs to me in a number of ways: email me, post source code in the comments section or post your design on your own website and send me the link – whatever you feel is best.
If you do not have access to a commercial maths package such as Mathematica, MAPLE or MATLAB then I suggest that you take a look at SAGE which is completely free (in fact you should take a look at SAGE even if you DO have one of the commercial systems).
Assuming some people actually respond to this post, I will post some of my favourites over the run up to Christmas.
Have fun!