Fibonacci numbers from matrix determinants
Many years ago (way WAY before the web), at the tender age of 10, I did a school math project about the Fibonacci numbers and got rather carried away with writing about the many different areas of mathematics and everyday life where this sequence popped up. Although I didn’t have the internet to help with my research, I did have a wonderful maths teacher called Ron Billington who taught for many years at Birchensale Middle School in Redditch. Mr Billington had a personal library of maths books that he collected over the years which was a treasure trove of material for someone like me who had significantly more enthusiasm than talent. He would have loved hearing about the little discovery I made while browsing through The College Mathematics Journal the other day.
First, a bit of background. The Fibonacci sequence starts off like this:
1 1 2 3 5 8 13 21
Each term in the sequence is formed from the sum of it’s two predecessors so the next term would be 13 + 21 = 34. What fascinated me as a child (and continues to fascinate me now) is the fact that this incredibly simple sequence of numbers, and others like it, seems to appear all over the place from the distribution of sunflower seeds to the study of photonic crystals.
There really is an astonishing amount of mathematics around the Fibonacci sequence as you will be able to verify with a quick google search. There is even an academic journal dedicated to the mathematics around it – The Fibonacci Quarterly – which I, unfortunately, have no access to at the moment (might have to have a word with the University librarian about that).
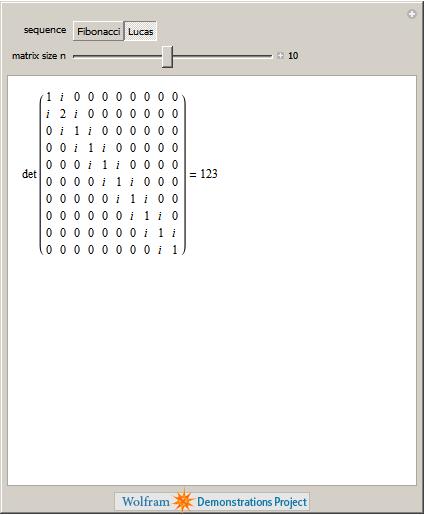
In the article Fibonacci Determinants, by Nathan Cahill et al (The College Mathematics Journal vol33 p221-225), the authors demonstrate the fact that you can obtain the nth term in the Fibonacci sequence by taking the determinant of a n x n tridiagonal matrix of the form

What’s more, if you change just a single entry (row 2 col 2) from 1 to 2 then you will obtain the Lucas Numbers instead. I thought that this was fun and so knocked up a Wolfram Demonstration for it which you can get to by clicking on the image below.
So Mr Billington – I have found yet another branch of Mathematics where the Fibonacci numbers turn up – Linear Algebra. I know it’s been 20 years but is there any chance of upping that B- to an A :) ?
If you enjoyed this article, feel free to click here to subscribe to my RSS Feed.

Just a note – I’m hosting the next Carnival of Mathematics at thoughtcounts.net tomorrow. The carnival page lists no host, so I have a lower than usual number of submissions. If you have anything to submit, I’d love to hear from you. (a@thoughtcounts.net)
Hi there! I was pleasantly surprised to see that someone enjoyed my CMJ article, let alone read it! Just wanted to drop a line to say that I became interested in the Fibonacci numbers at around age 10 as well, after watching the “Case of the Willing Parrot” episode of Square One TV’s Mathnet.
Hi Nathan
So good to hear from you. I thought the CMJ article was great – such a great result and at a level that I could actually follow :)
The Wolfram Demonstration turned out to be reasonably popular too and I have had a few comments about it – mainly along the lines of ‘cool result;. Just a shame it’s not MY result ;)
Best wishes,
Mike