Fractals on Wolfram Alpha – an update
Back in May 2009, just after Wolfram Alpha was released, I had a look to see which fractals had been implemented. Even at that very early stage there were a lot of very nice fractals that Wolfram Alpha could generate but I managed to come up with a list of fractals that Wolfram Alpha appeared to know about but couldn’t actually render.
On a whim I recently revisited that list and am very pleased to note that every single one of them has now been fully implemented! Very nice.
Can you find any Wolfram Alpha fractals that I missed in the original post?

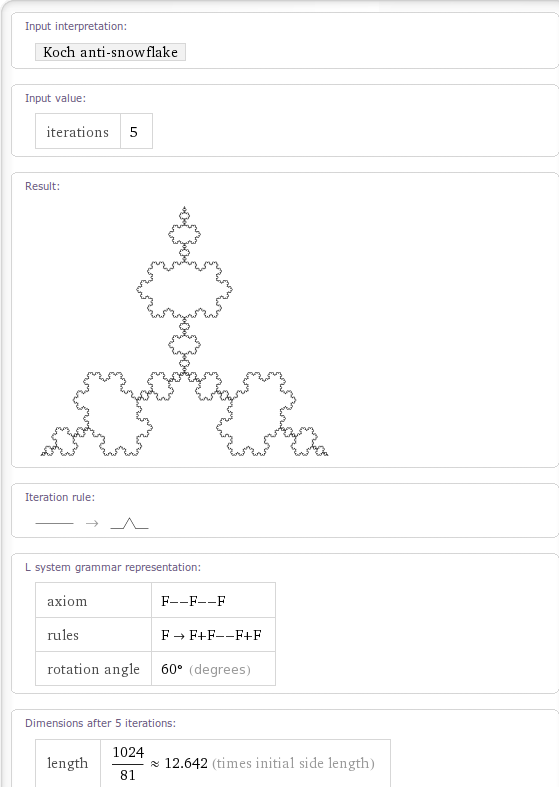
i tried this on my python L-system but had to change the axiom to “F++F++F”
from turtle import left, right, forward, hideturtle, tracer, color,colormode tracer(10) hideturtle() #draws the L-system acorrding to patern def draw(patern,size,rot): #right(270) for char in patern: if char == "F": forward(size) if char == "+": right(rot) if char == "-": left(rot) def iterate(n,axiom,rules,size,rot): if n>0: axiom = produce(axiom,rules) return iterate(n-1,axiom,rules,size,rot) else: return draw(axiom,size,rot) def produce(axiom,rules): output = "" for i in axiom: output = output + rules.get(i,i) return output #iterate(15,"FX",{'X':'X+YF+','Y':'-FX-Y'},3,90) iterate(7,"F++F++F",{'F':'F+F--F+F'},1,-60)My favorite implementation of the koch snowflake would be:
a=Exp[Pi/3I];b=Nest[{#,a#,a\[Conjugate]#, #}/3&,1,5];{Re[#],Im[#]}&/@Accumulate[Flatten[{0,a b,a\[Conjugate]b,-b}]]//Line//Graphics
Also have a look at: http://www.remcobloemen.nl/2009/12/complex-analysis-l-systems-and-christmas/ very nice stuff :-)